式と宣言
このページでは,式,宣言,変数束縛などに関する基本的なトピックスを説明します.
1. 変数の束縛
変数を値に結びつけることを,変数の 束縛(binding)といいます. 変数の束縛は次のように書きます.
変数名 = 式次のプログラムは,変数 m を値 123 に,変数 n を値 456 にそれぞれ束縛します.
m = 123 -- 変数 n を値 123 に束縛
n = 456 -- 変数 n を値 456 に束縛
main = do print m -- 出力: 123
print n -- 出力: 456変数の束縛は,必ずしもその変数を使う場所より前に書く必要はありません. よって,このプログラムは次のように書くこともできます.
main = do print m -- 出力: 123
print n -- 出力: 456
m = 123
n = 456同名の変数の再定義は許されません. よって,次のようなコードを含むプログラムはコンパイルエラーとなります.
n = 123
n = 456|
プログラミング言語の入門書で,よく変数を "箱" に喩えて説明しているのを見ますが,Haskell ではその発想は切り替えた方がいいかもしれません. Haskell における変数は,"代入" という概念が存在せず,値に名前をつける役割しかもちません. そのため,"箱" よりかは "名札" とか "タグ" みたいなイメージがぴったりな気がします. 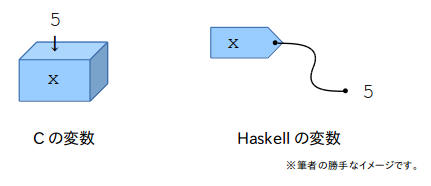
|
2. 型注釈
Haskell には強力な型推論機構があるため,変数や関数の定義に型を書く必要はありません. ただし,プログラマやコンパイラにヒントを与える目的で,型を明示するケースもしばしばあります.
変数や関数の型を明示するには,型注釈を書きます.
m, n :: Int -- "変数 m, n の型は Int" と宣言
m = 1 + 2
n = 2 + 3
main = do print m
print n型の明示は,次のように式に対して行うこともできます.
n = 2 + 3 :: Int -- "式 2 + 3 の型は Int"
main = print n3. パターン
変数の束縛は,パターン (pattern) を利用した次の形で行うこともできます.
パターン = 式次のプログラムは,パターンによる変数束縛を利用した例です.
(a, b, c) = (123, 3.14, "hello")
main = do
print a -- 出力: 123
print b -- 出力: 3.14
print c -- 出力: "hello"パターンを使ったいろいろな変数束縛の例を示します.
(a, b, c) = (123, 3.14, "hello")
[a, b, c] = [1, 2, 3]
Just x = Just 123
(a, _, _) = (123, 3.14, "hello")この最後の例は,ワイルドカードと呼ばれるパターン _ を利用しています.
ワイルドカードは,関心のない値を無視するときに使います.
パターンによる変数束縛とふつうの変数束縛を両方やりたいという欲張りなプログラマのために,アズパターン (as pattern) という構文も提供されています.
次の例のように 変数 @ パターン という形式で使います.
t@(a, b, c) = (123, 3.14, "hello")
main = do
print a -- 出力: 123
print b -- 出力: 3.14
print c -- 出力: "hello"
print t -- 出力: (123, 3.14, "hello")パターンの中に書けるのは,変数,ワイルドカードと,値構成子("代数的データ型" のページで説明)です. 当然と言えば当然なのですが,パターンの中に関数や演算子を書くことはできないので,注意しましょう.
|
余談ですが,ちょっと昔の Haskell では次のようなパターンも許されてました(現在でも このパターンは n + k パターンとよばれています. 恐らくペアノ数のパターンマッチングにならって導入されたものだと思いますが,不評だったのか,Haskell 2010 で仕様から削除されてしまいました…. |
4. パターンマッチング(case 式)
パターンマッチング(pattern matching)とは,式の値がパターンにマッチするかしないかを判定する仕組みです. 日本語で "パターン照合" ともよばれます. パターンマッチングを利用することで,プログラムでどの式を評価するかを,パターンに応じて切り替えることができます.
次のプログラムは,パターンマッチングを利用した関数 getValue を定義したものです.
getValue defval maybe は,Maybe 型の値 maybe が Nothing ならばデフォルトの値 defval を,Just x ならば x を返す関数です.
getValue defval maybe =
case maybe of
Nothing -> defval
Just x -> x
main = do
print (getValue 0 Nothing) -- 出力: 0
print (getValue 0 (Just 5)) -- 出力: 5case 式は,パターンマッチングによって評価する式を切り替えるために使われます.
C の switch 文と似たような機構です.
一般形は次の通りです.
case 式 of { パターン1 -> 式1 ; ... ; パターンn -> 式n }式が パターンi にマッチしたとき,式i がこの case 式全体の値になります.
case 式内のパターンの順番は意味があります.
パターン1,パターン2,…と調べていって,最初にマッチしたパターンの式が採用されます.
ですので,次のようなプログラムを書いたとき,最後の行はまったく無意味です(コンパイルは通りますが警告が出ます).
getValue defval maybe =
case maybe of
_ -> defval -- ここですべてマッチしてしまう
Just x -> x -- ここには到達しない!5. ガード(case 式)
ガード(guard)は,パターンマッチングに加えて論理(条件式)で式の評価を制御する仕組みです.
パターンの後に,縦棒(|)区切りで条件式を記述します.
次のプログラムのように使います.
absMaybe x =
case x of
Nothing -> 0
Just x | x < 0 -> -x -- Just x にマッチし,x < 0 のとき
| otherwise -> x -- Just x にマッチし,x < 0 でないとき
main = do
print (absMaybe Nothing) -- 出力: 0
print (absMaybe (Just 5)) -- 出力: 5
print (absMaybe (Just (-5))) -- 出力: 5otherwise はどんな条件でも成立する論理式です.
実際,otherwise は True と等価です.
6. if 式
次のプログラムは,絶対値を求める関数 abs を定義したものです.
abs x = if x < 0 then -x else x
main = print (absolute (-5)) -- 出力: 5一般に,if 式は次のように書きます.
if 条件式 then 式1 else 式2if 式は文ではなく式なので,値をもちます.
そのため,式1 はおろか,式2 を省略することはできません.
また,式1 と 式2 は型が同じでなければなりません.
|
鋭い方はすでにお気づきかもしれませんが, |
7. let 式
次の let 式は,変数や補助関数を局所的に定義するのに用いられます.
let { 宣言1 ; ... ; 宣言n } in 式宣言i で定義した変数または関数は,変数i+1 以降と 式 にのみスコープを持ちます.
そして,式 がこの let 式全体の値となります.
次のプログラムは,半径 r の円の面積を求める関数 area を定義したものです.
let 式の中で局所定義された pi と square は,その let 式の中だけで有効です.
area r =
let pi = 3.14
square x = x * x
in pi * square r
main = print (area 10.0) -- 出力: 314.08. where 節
変数や補助関数を局所的に定義する方法には,where 節を使う方法もあります.
where { 宣言1 ; ... ; 宣言n }次のプログラムは,先と同様の関数 area を where 節を用いて書き換えたものです.
area r = pi * square r
where
pi = 3.14
square x = x * x
main = print (area 10.0) -- 出力: 314.0